Low Pass Filtering Calculator, Simulation, and Theory
Lowpass filtering can be achieved with a simple RC Low pass filter (LPF). RC low pass filters are circuits that allow lower frequencies to pass through while blocking higher frequencies. This can be useful in may applications like filtering out the higher frequencies music signal to a bass speaker (speaker designed to produce low frequencies). Additionally these filters can remove unwanted noise from a circuit.
RC Low Pass Filter Calculator
For more information on how to use this online calculator view the documentation here
Resistor Calculator
Capacitor Calculator
RC Low Pass Filter
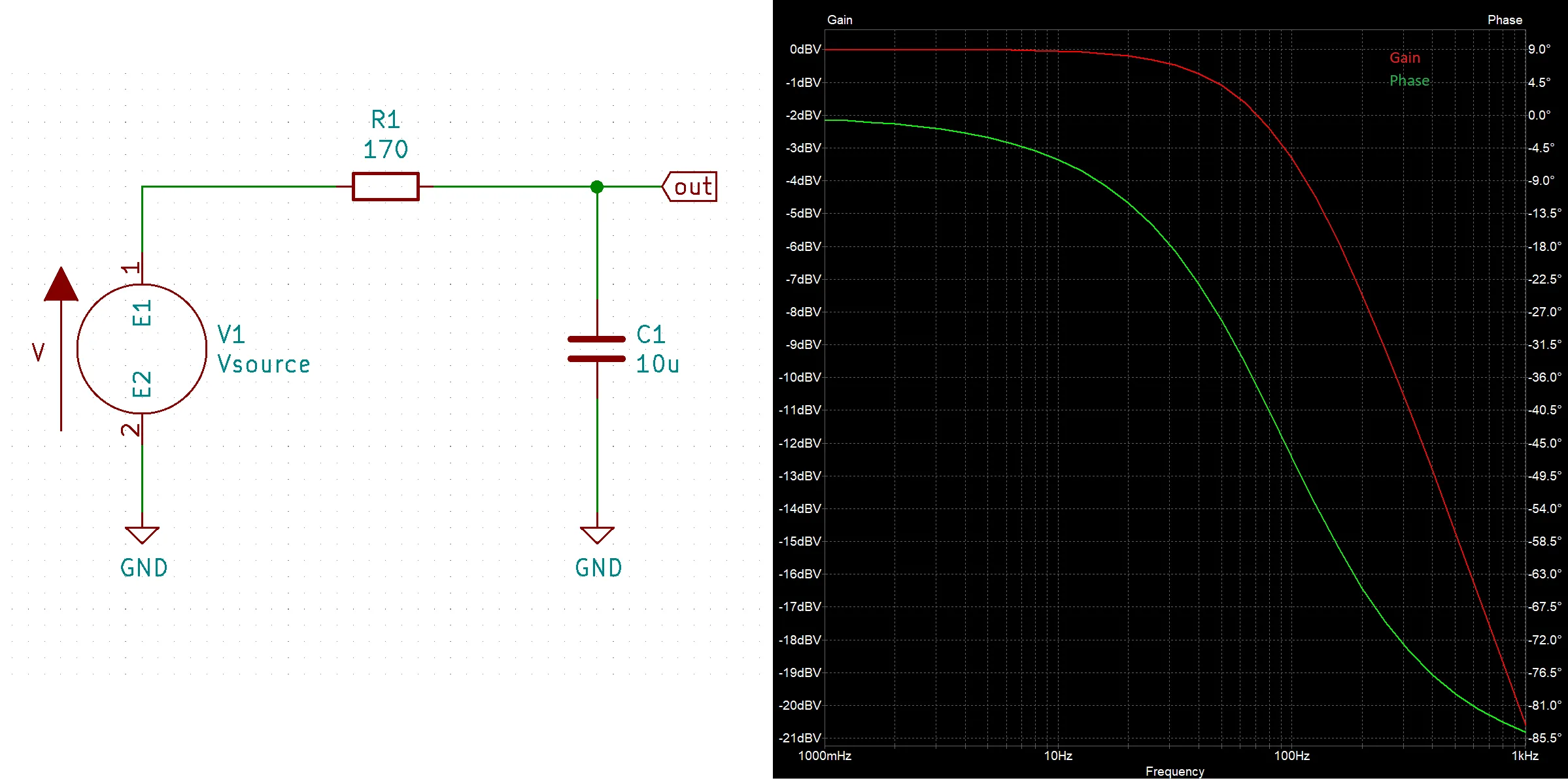
The simplest LPF circuit is the RC low pass filter. This LPF is just a resistor in series with a capacitor where the output is taken in between the two components.
The basic idea for how this filter works is at low frequencies the capacitor $C_1$ acts like a open and therefor making the output equal to the input. Conversely, at high frequencies the capacitor $C_1$ acts like a short so that the entire input signal is shorted to ground and making the output equal zero.
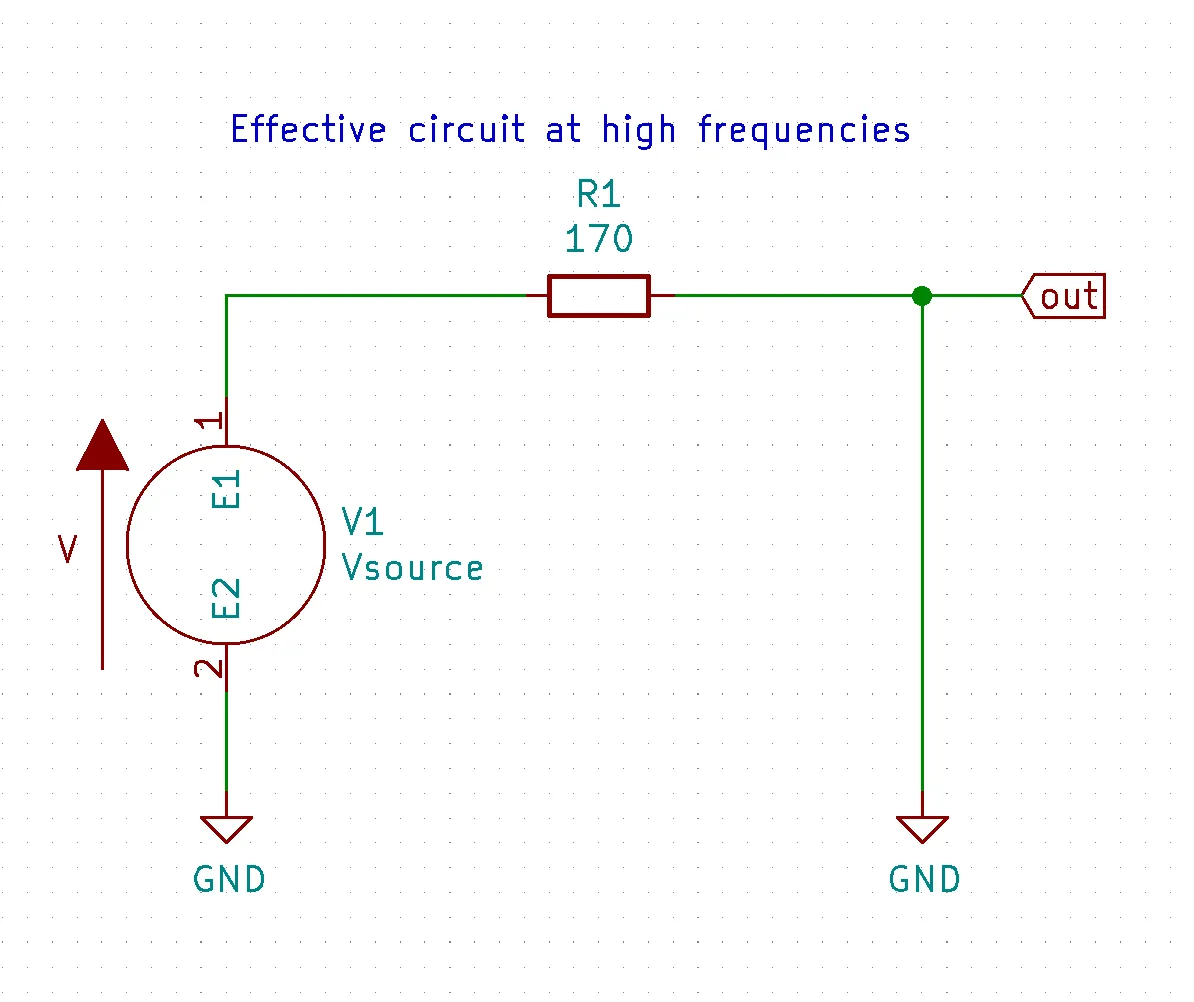
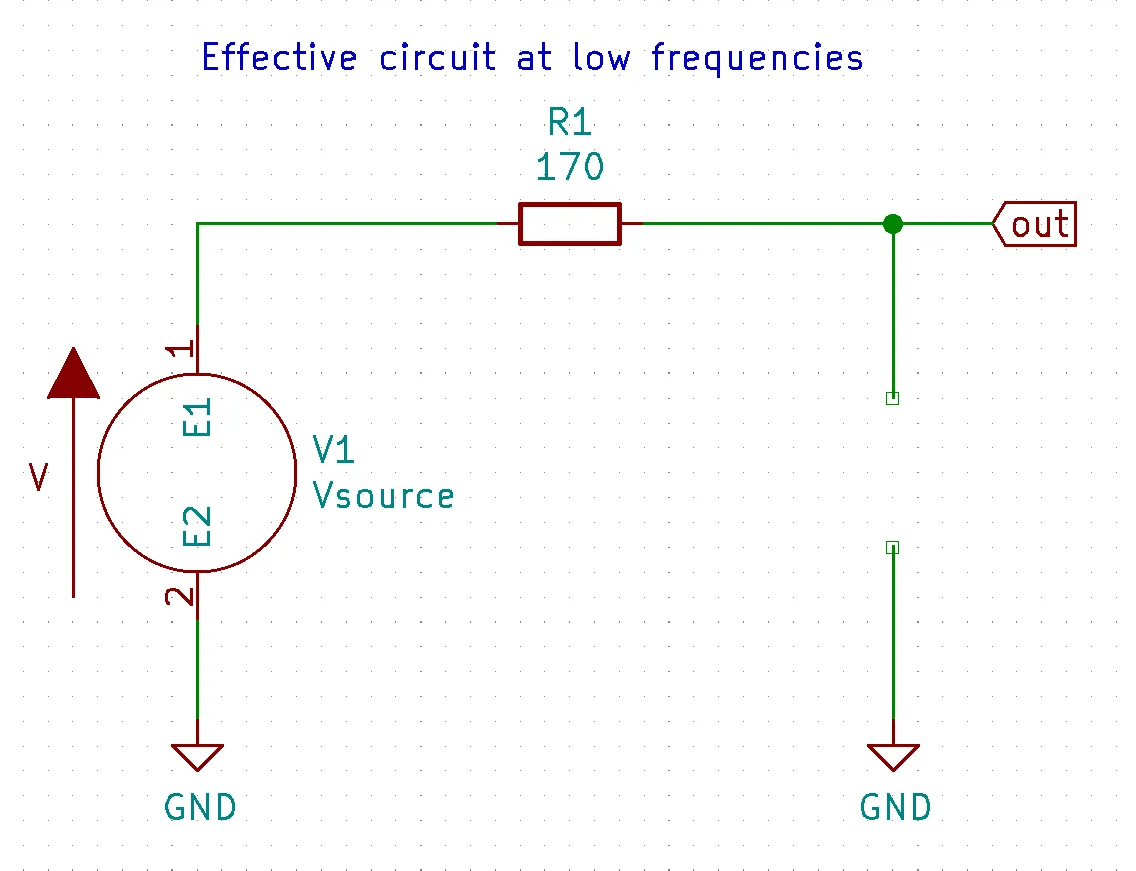
Below is a video of us demonstrating how to do a KiCad simulation of an RC LPF circuit.
RC Low Pass Filter Simulation (Video)
This is a video demonstrates lowpass filtering with KiCad. In the video we create a low pass filter simulation and show the effects of adjusting the resistor and capacitor in an RC low pass filter.
Theory (Approximation)
For the RC LPF approximation equation just use $X_{C_1}$ for the capacitor and treat it like a resistor. Below is the equation for a voltage divider
$$V_{out} = V_{in}{X_{C_1} \over{X_{C_1} + R_1}}$$
$$\boxed{V_{out} = V_{in}{{1 \over(2 \pi f C_1)} \over{{1 \over(2 \pi f C_1)} + R_1}}}$$
At high frequencies
Using the capacitive reactance equation we can see that as frequency goes up $\uparrow f \Rightarrow {1 \over(2\pi (f \uparrow ) C_1)}\downarrow \Rightarrow X_{C_1} \downarrow$ and at a high enough frequency $X_{C_1} \approx 0$. When this happens the RC LPF equation turns into $V_{out} \approx V_{in} {0\over 0 + R_1} \Rightarrow V_{out} \approx 0$ thus blocks all higher frequencies
$$V_{out} = V_{in} {\downarrow X_{C_1} \over \downarrow X_{C_1} + R_1} \approx V_{in}{0 \over 0 + R_1} \approx 0$$
$$\boxed{V_{out} \approx 0}$$
At low frequencies
Conversely, as frequency goes down $\downarrow f \Rightarrow {1 \over(2\pi (f \downarrow ) C_1)}\uparrow \Rightarrow X_{C_1} \uparrow$ and at a low enough frequency $X_{C_1} \gg R_1$ so we can ignore $R_1$ because $X_{C_1}$ is the dominant factor. When this happens the RC LPF equation turns into $V_{out} \approx V_{in} \cancel{X_{c_1}\over X_{c_1}} \Rightarrow V_{out} \approx V_{in}$ thus passes all lower frequencies
$$V_{out} = V_{in} {\uparrow X_{C_1} \over \uparrow X_{C_1} + R_1} \approx V_{in}\cancel{X_{C_1} \over X_{C_1}} \approx V_{in}$$
$$\boxed{V_{out} \approx V_{in}}$$
Theory (Complex solution)
The complex solution uses $X_{C_1} = {j \over {w C_1 }}$ instead of $X_{C_1} = {1 \over {w C_1}}$ where $w = 2 \pi f$
$$V_{out} = V_{in}{{j \over{w C_1}}\over{{j \over{w C_1}} + R_1}} = V_{in}{j \over{C_1 R_1 w + j}}$$
taking the absolute value of a complex number will give us its magnitude. Meaning if we take the absolute value we will get the amplitude and not worry about the phase.
$$\boxed{V_{out} = V_{in}{1 \over{\sqrt{{R_1^2w^2 C_1^2}+1}}}}$$
Lowpass Filtering Usages
Filter out high frequency noise
High frequency noise can be filtered out with a low pass filter allowing for a cleaner output wave form.
Filter out high frequency signals
In the cause of audio, the higher frequency audio can be filtered out leaving on the bass frequencies that can then be passed to a subwoofer